
1.4장 내용 정리 + 연습문제 풀이입니다.
연습문제 풀이의 경우 모든 문제를 풀이하지만 간단하거나 조금 이상한 문제는 스킵하기도 합니다.
풀이에서 나오는 기호들을 모르시겠다면 이 글을 한번 보시고, 궁금한 점이 있다면 댓글로 남겨주세요.
영어로 된 수학 용어 정리
해석학 수업 교재가 그 유명한 Wade라서 모든 지식을 영어로 배워야하는데요. 생전 처음보는 원서이기에 모르는 단어들이 너무 많아, 공부한 단어들을 여기 적어놓습니다. 찾으시려면 컨트롤 F
takiya9215.tistory.com
1.4. 역함수, 역삼각함수와 역쌍곡선함수
1. 역함수
함수 f가 집합 X에서 Y로 대응되는 함수일 떄 함수 \(g : Y \to X\)가 존재하여
(a) 모든 y \(\in Y \) 에 대하여 f(g(y)) = y이고,
(b) 모든 x \(\in X \) 에 대하여 g(f(x)) = x일 때
g를 함수 f의 역함수라고 부르고, \(g=f^{-1} \)로 표기한다.
말이 어렵지만 결론은 뭐냐면 f(x)가 전단사 함수일 때 역함수가 존재한다는 내용입니다.
- 전사 함수 = 일대일 함수 : \( x_1 \neq x_2 \to f(x_1) \neq f(x_2) \)
- 단사 함수 = 공역이 치역과 같은 함수
여기서 \(f : X \to Y\)가 아닌 \(f : X \to f(X) \)인 경우 함수 f가 역함수를 가질 필요충분조건은 일대일 함수가 됩니다.

가령 예를 들어서 위 그림처럼 함수 f:X->Y가 있고 이를 역함수로 나타내어봤을 때, c는 집합 Y에 있는 원소로서 \(f^{-1}\)의 정의역에 포함되지만 함숫값이 없죠. 따라서 역함수가 존재할 수 없게 되는 것입니다. 공역과 치역이 다르기 때문에 생기는 현상입니다.
하지만 함수 f의 공역을 집합 Y의 부분집합인 f(X), 즉 치역으로 제한해주면

이렇게 함수 f는 전사함수가 되고, 역함수가 존재할 수 있게 되는 것입니다. 근데 사실 복잡하게 생각하실 것 없이 그냥 수평선 판정법 패스하면 역함수라고 보셔도 무방합니다..
함수가 역함수를 가지는지 가지지 않는지를 판정하는 수평선 판정법은 x축에 수직인 직선을 그어서 위 아래로 움직여보면서, 해당 직선과 함수의 그래프의 교점이 2개 이상 생긴다면, 해당 함수는 전사함수가 아니므로 역함수가 존재하지 않는다! 라고 판정하는 기법입니다.
추가적으로, 구간에서 증가, 감소하는 증가함수나 감소함수는 역함수를 가집니다.
2. 역삼각함수
삼각함수는 기본적으로 주기를 가지기 때문에 실수 전체에서는 전사함수라고 할 수 없습니다. 그렇기 때문에 정의역을 제한해서, 일대일 함수를 만들어준 뒤 역함수를 취하게 됩니다.





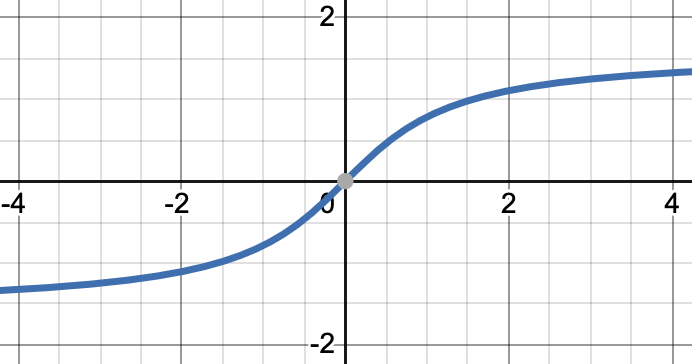
함수의 정의역, 치역은 교재를 참고하시면 되겠습니다.
3. 역쌍곡선함수
1.3장에서 배운 쌍곡선 함수의 역함수입니다. 삼각함수와는 달리 역함수를 양함수로 표현할 수 있습니다.
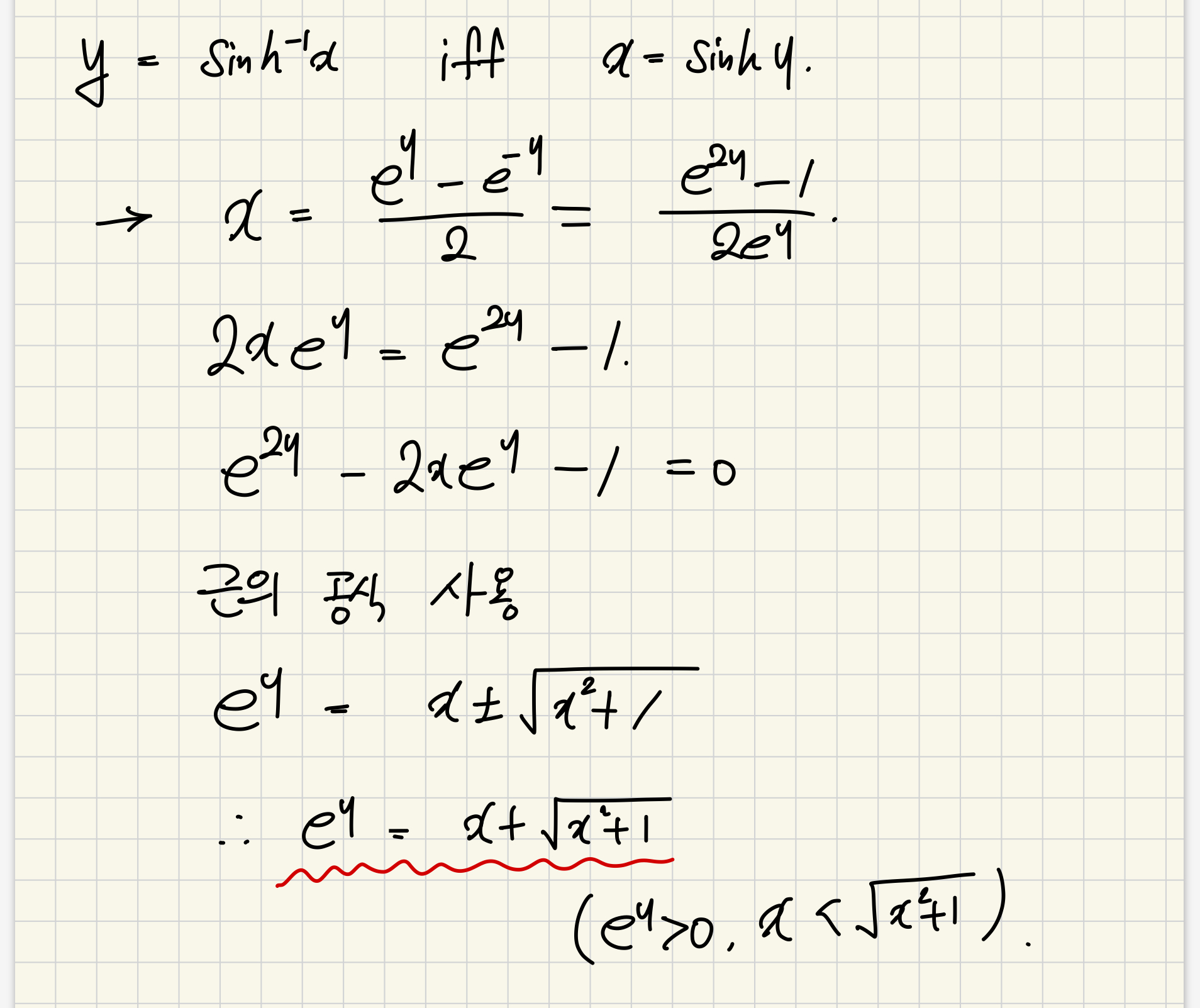
증명은 이렇게 하시면 됩니다. (iff는 필요충분조건입니다.)
연습문제 풀이






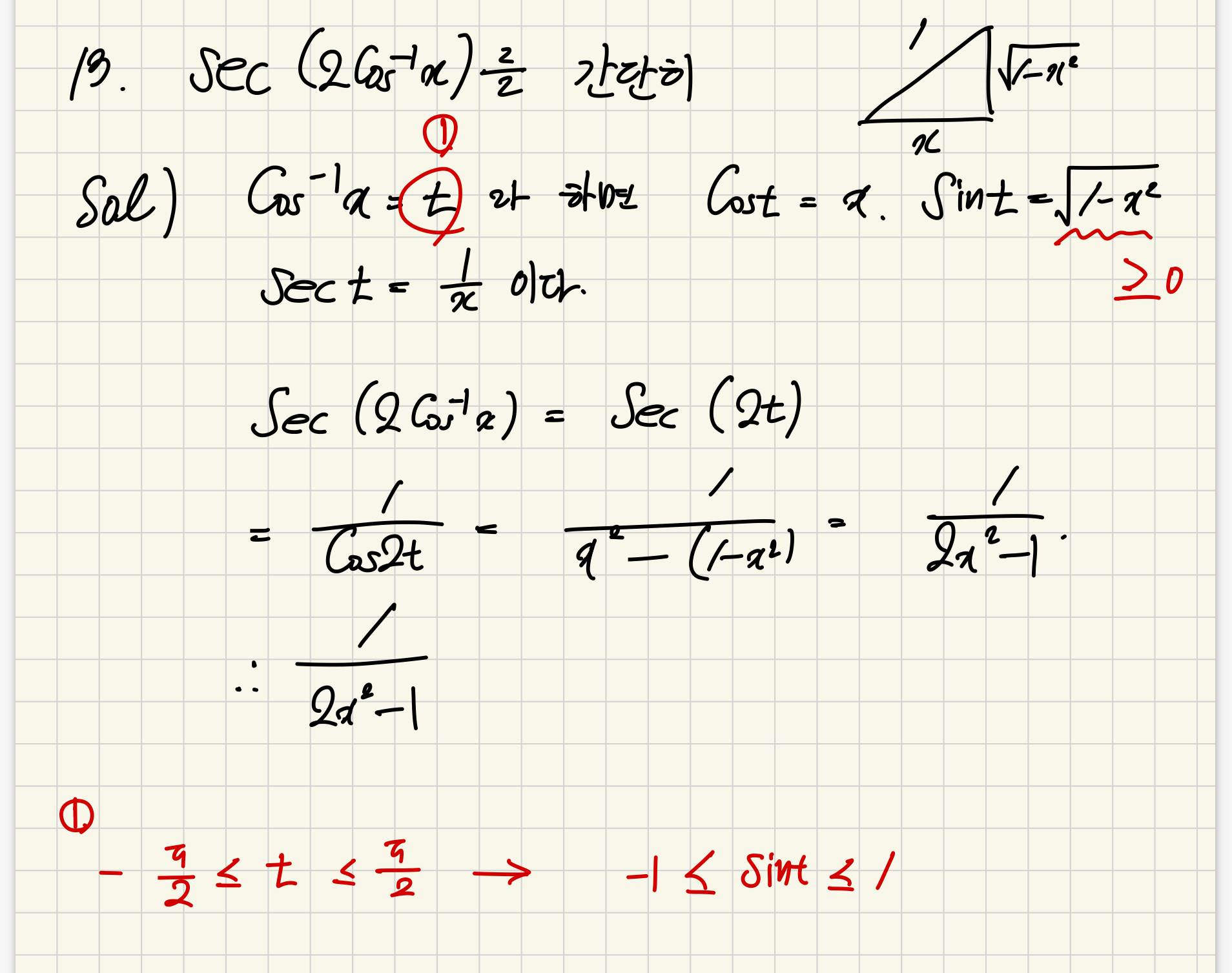
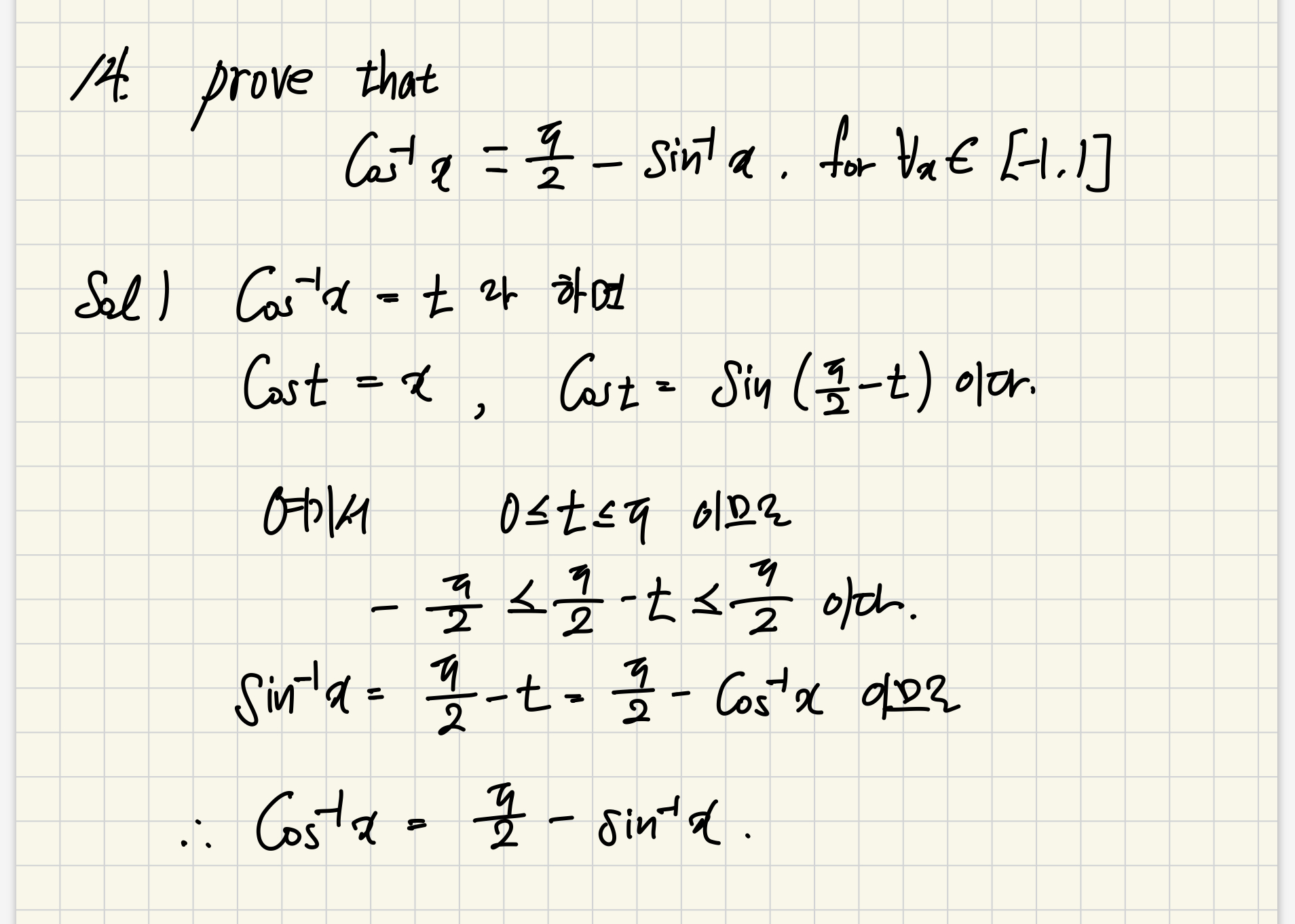
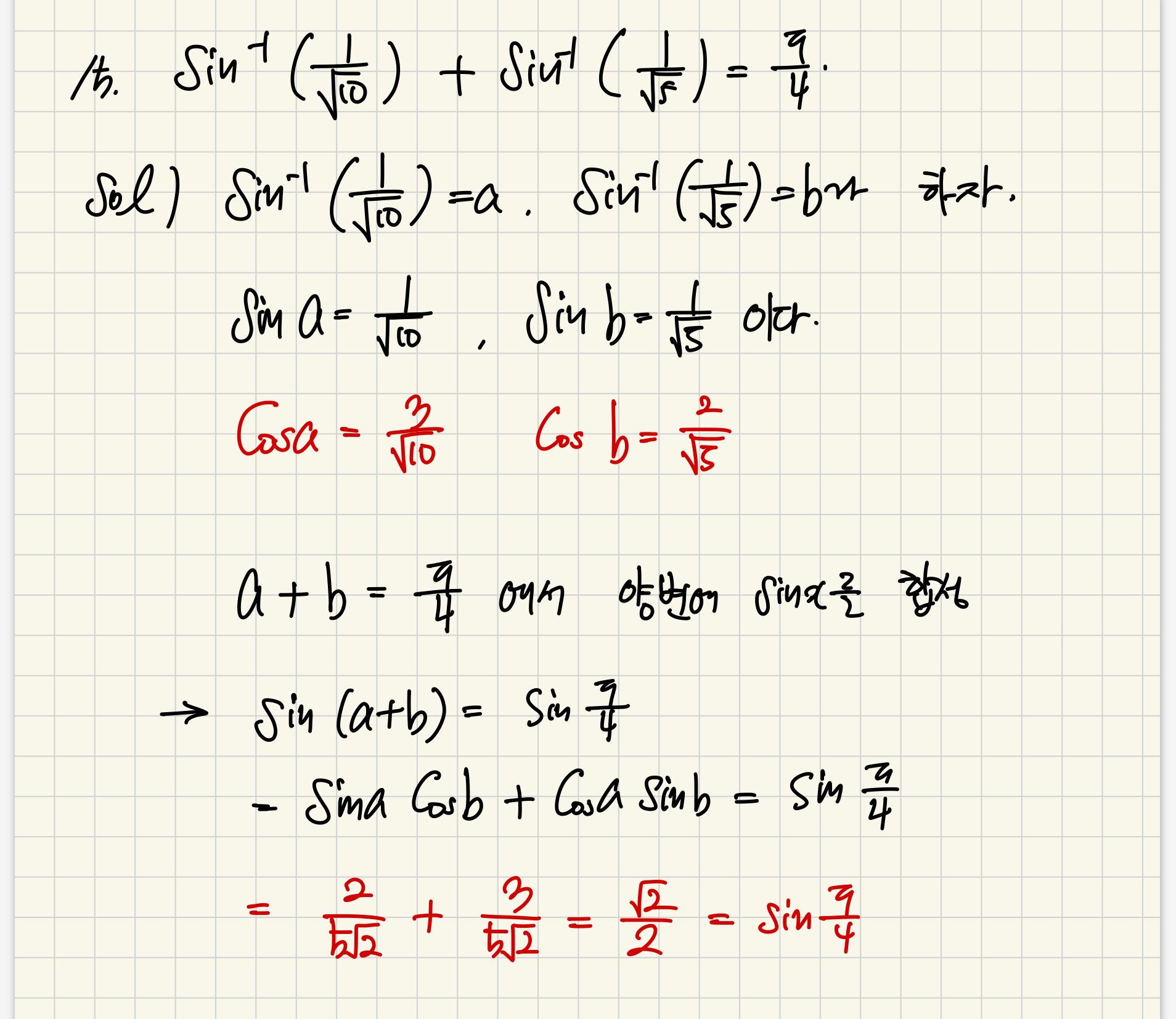
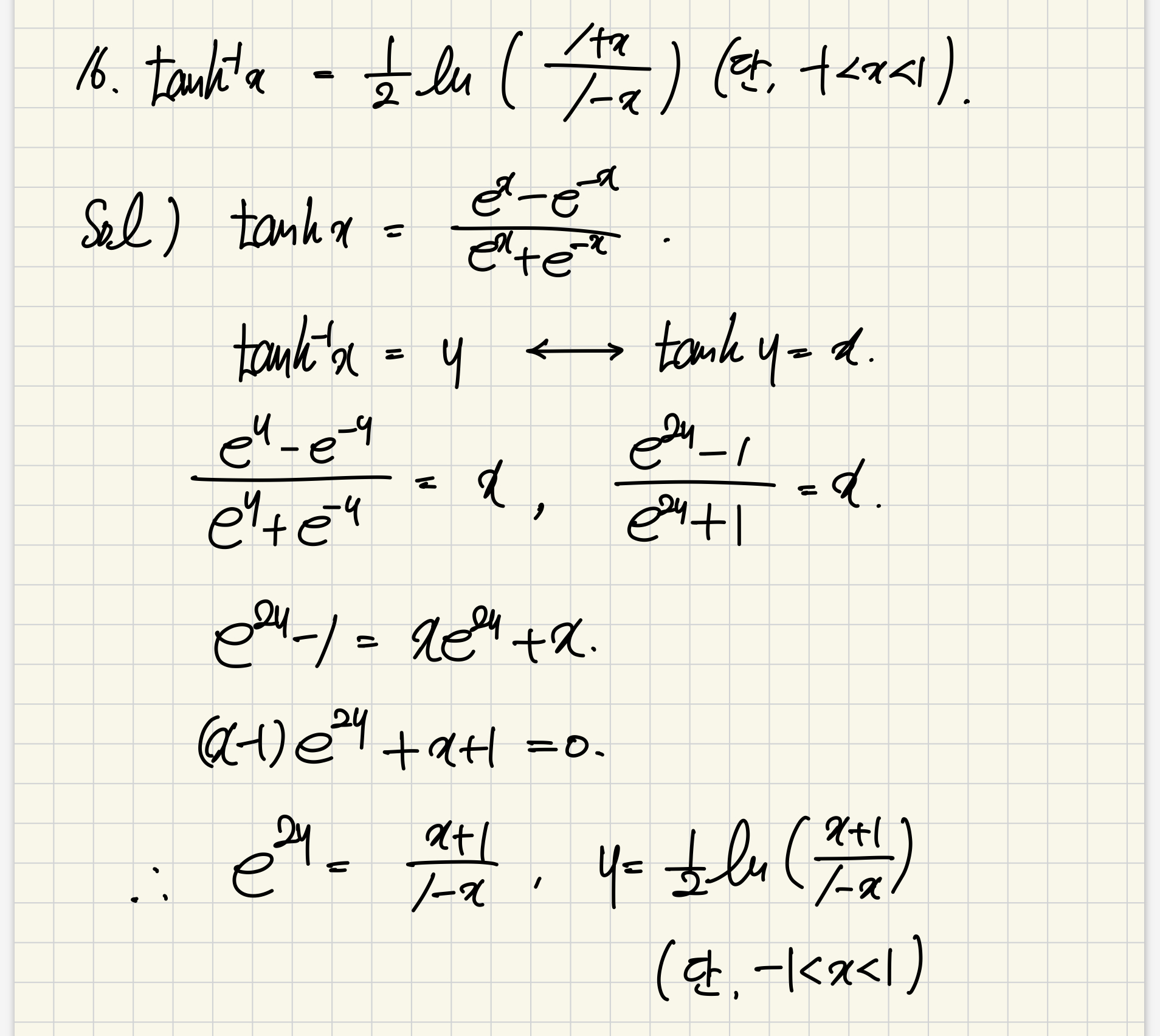
'25년 1학기 > 미분적분학' 카테고리의 다른 글
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 2.2장 정리 + 솔루션 (0) | 2025.04.02 |
|---|---|
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 2.1장 정리 + 솔루션 (0) | 2025.04.02 |
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 1.3장 솔루션 (0) | 2025.03.16 |
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 1.2장 솔루션 (0) | 2025.03.16 |
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 1.1장 솔루션 (0) | 2025.03.16 |