
1.4장 내용 정리 + 연습문제 풀이입니다.
연습문제 풀이의 경우 모든 문제를 풀이하지만 간단하거나 조금 이상한 문제는 스킵하기도 합니다.
풀이에서 나오는 기호들을 모르시겠다면 이 글을 한번 보시고, 궁금한 점이 있다면 댓글로 남겨주세요.
영어로 된 수학 용어 정리
해석학 수업 교재가 그 유명한 Wade라서 모든 지식을 영어로 배워야하는데요. 생전 처음보는 원서이기에 모르는 단어들이 너무 많아, 공부한 단어들을 여기 적어놓습니다. 찾으시려면 컨트롤 F
takiya9215.tistory.com
제거가능 불연속

이 함수처럼 함숫값을 극한값으로 정의해서 불연속 점을 제거할 수 있으면 제거가능 불연속입니다.

f(x)-> L as x->c일 때 g가 x=L에서 연속이면 리미트를 g(x)안으로 집어넣을 수 있습니다.
무작정 리미트를 g(x) 안으로 집어넣으면 안됩니다. 항상 정리를 사용할 수 있는 조건이 갖춰져있는지 확인해야합니다. 또한 f(x)가 x=c 에서 정의되어야할 필요도 없습니다. 극한이기 때문입니다.
사잇값 정리
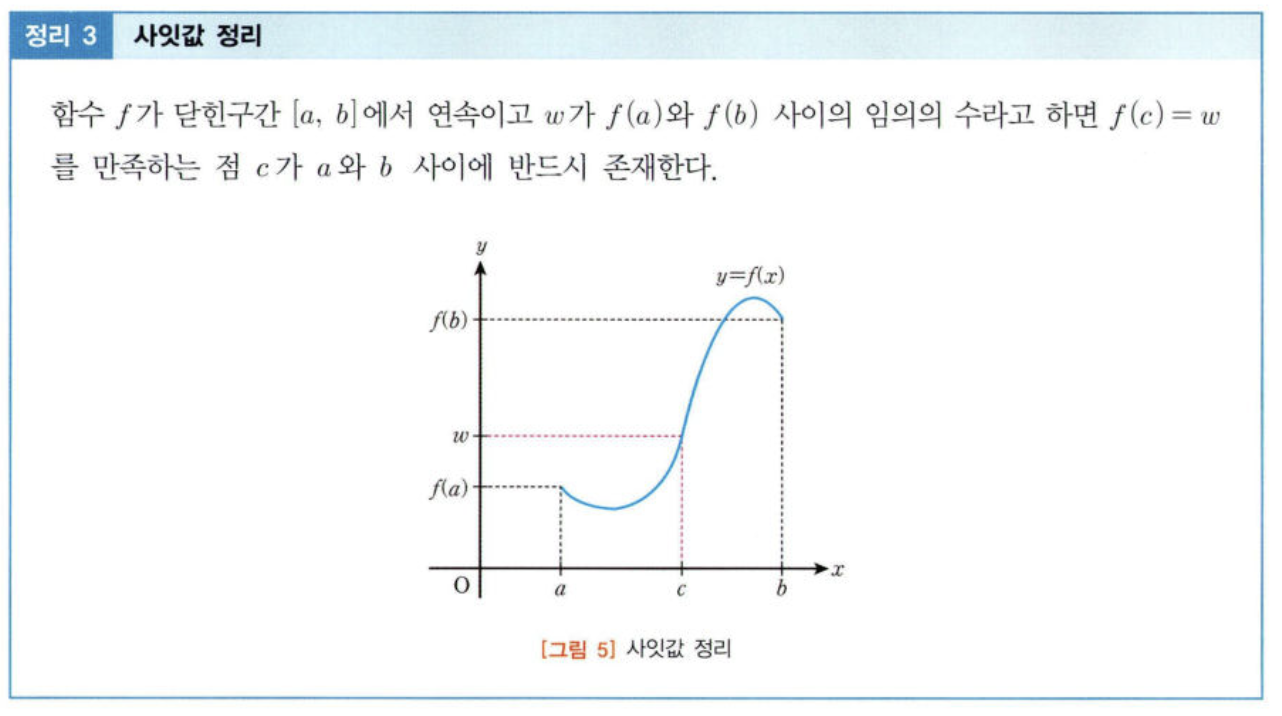
고등학생 때 배웠던 사잇값 정리입니다.
이 정리를 증명하기 위해서는 해석학 지식이 필요하기에 아마도 증명까지는 배우지 않았던 것으로 기억합니다.
그래도 혹시 궁금하신 분을 위해 링크를 달아둡니다.
고등학교 과정에서 사이값(중간값) 정리의 증명
고등학교에서는 극한을 정확하게 다루기 어렵기 때문에 그와 관련된 내용은 증명하지 않고 넘어가는 ...
blog.naver.com
닫힌구간에서 분명히 연속이어야합니다.
(a,b)에서 함수 f(x)가 연속이고 함숫값 f(a)와 x=a에서의 우극한, f(b)에서의 함숫값과 x=b에서의 좌극한이 같으면 닫힌 구간에서 연속입니다.
이분법

이분법 예시입니다. 사람 손으로 하게 될 일은 아마 예제를 풀 때 말고는 없겠지만, 그럼에도 불구하고 뭔지는 알아야합니다.
간단히 말해서, 구간 [1,2]에 근이 존재할경우, 해당 구간을 둘로 나눠 다시 조사해보는 것입니다. 가령 [1,3/2], [3/2,2] 이렇게요.
그러면 근이 존재하는 구간이 선택될 것이고, 그러면 다시 그 구간을 반으로 나눠서 같은 과정을 반복합니다.
최대 최소 정리

f(a), f(b)등 함숫값을 상, image라고도 합니다.
f(x)가 연속이면 이 image 집합에서는 항상 최대와 최소가 있다는 것이 이 정리의 내용입니다. 역시나 닫힌 구간에서 연속이라는 조건을 충족해야합니다.
증명은 해석학적 내용을 알아야 할 수 있기 때문에 여기 적어놓지는 않겠습니다.
연습 문제 풀이



'25년 1학기 > 미분적분학' 카테고리의 다른 글
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 3.2장 정리 + 솔루션 (0) | 2025.04.05 |
|---|---|
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 3.1장 정리 + 솔루션 (0) | 2025.04.05 |
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 2.1장 정리 + 솔루션 (0) | 2025.04.02 |
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 1.4장 정리 + 솔루션 (0) | 2025.03.17 |
| 미분적분학 - 기초부터 응용까지 (한빛아카데미) | 1.3장 솔루션 (0) | 2025.03.16 |